++ 50 ++ triangle calculator 30 60 90 triangle rules 328465

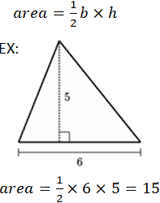
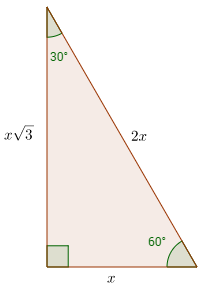
 The side which is opposite to the 30 degree angle will always have the shortest length The side opposite the 60 degree angle will be √3 times as long The side opposite the 90 degree angle will be twice as longArea of a Triangle The formula to calculate the area of a triangle is = (1/2) × base × height In a rightangled triangle, the height is the perpendicular of the triangle Thus, the formula to calculate the area of a rightangle triangle is = (1/2) × base × perpendicular Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)

Triangle Calculator

Triangle calculator 30 60 90 triangle rules

Triangle calculator 30 60 90 triangle rules-In a Euclidean space, the sum of angles of a triangle equals the straight angle (180 degrees, π radians, two right angles, or a halfturn) A triangle has three angles, one at each vertex, bounded by a pair of adjacent sides What is the shortest side of a 30 60 90 triangle?Tips for Remembering the Rules Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°)

Triangle Calculator

What are the side lengths of a 30 60 90 Triangle?30 60 90 and 45 45 90 Triangle Calculator I N S T R U C T I O N S Start by entering the length of a triangle side Then click on which type of side it is The 5 choices you have are As soon as you click that box, the output boxes will automatically get filled in by the calculator Clicking "RESET" clears all of the boxesRight Triangle Calculator Excel Details The 45°45°90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°45°90°, follow a ratio of 11√ 2Like the 30°60°90° triangle, knowing one side length allows you to determine the lengths of the other sides

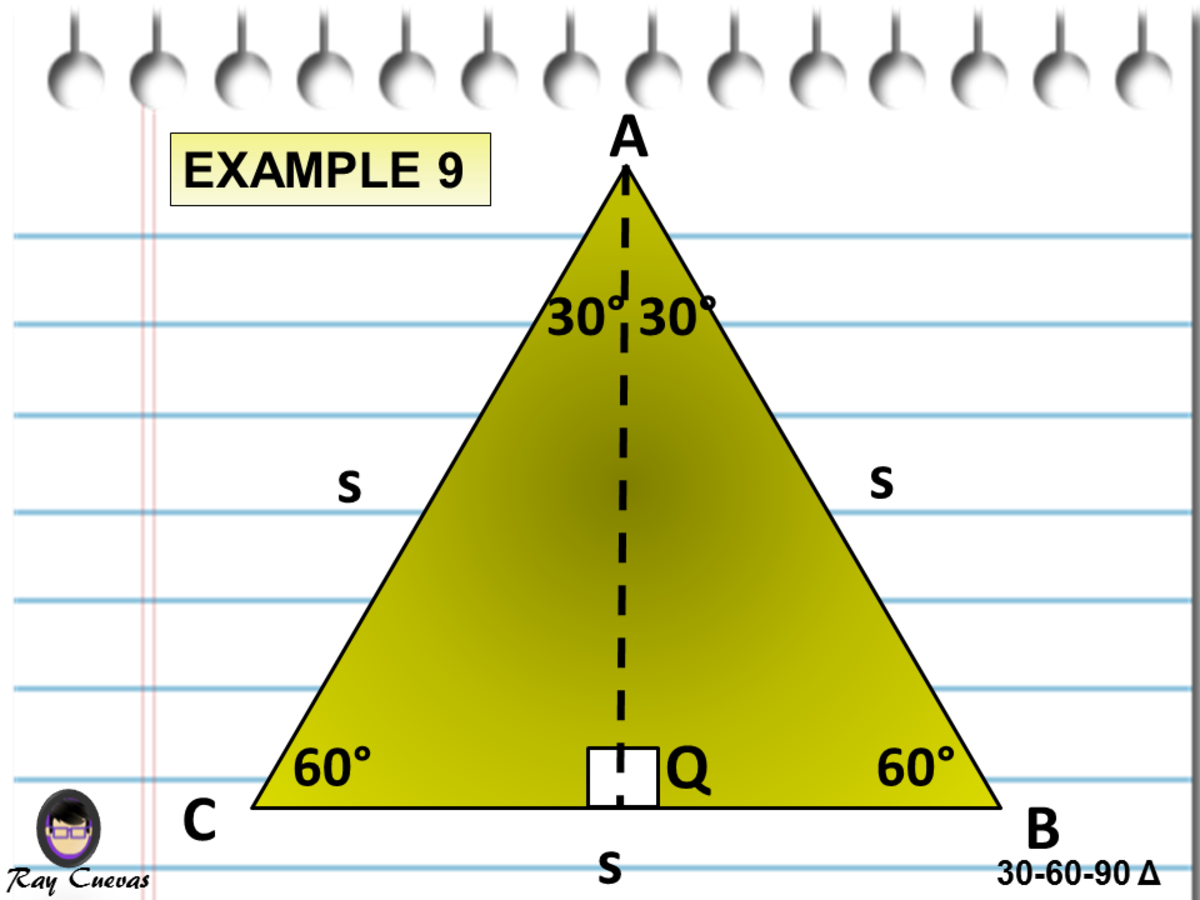
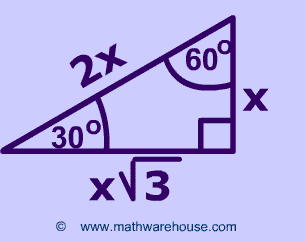
After this, press Solve Triangle 2) In addition, the calculator will allow you to same as Step 1 with a right triangle For this calculation, you would enter your 1 side on the 2nd picture marked and press Solve Triangle Simply enter the one side of the respective right triangle you know located by the picture and press the appropriate SolveMultiply this answer by the square root of 3 to find the long leg Type 3 You know the long leg (the side across from the 60degree angle) Divide this side by the square root of 3 to find the short side Double that figure to find the hypotenuse Finding the other sides of a triangle when you know the hypotenuseThe ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3

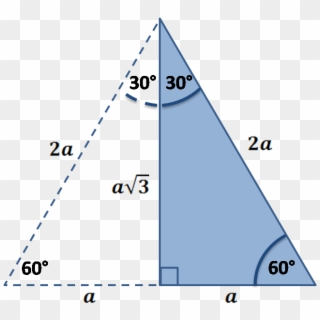
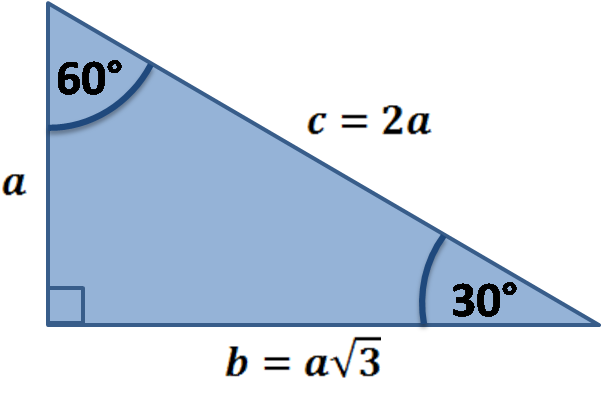
 Qualities of a Triangle A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle 30 60 90 triangle sides If we know the shorter leg length a, we can find out that b = a√3 c = 2a If the longer leg length b is the one parameter given, then a = b√3/3 c = 2b√3/3 For hypotenuse c known, the legs formulas look as follows a = c/2 b = c√3/2 Or simply type your given values and the 30 60 90 triangle calculator will do the rest! Remembering the triangle rules is a matter of remembering the ratio of 1 √3 2, and knowing that the shortest side length is always opposite the shortest angle (30°) and the longest side length is always opposite the largest angle (90°) Some people memorize the ratio by saying "x, 2x, x √3," because the "1, 2, 3

A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

30 60 90 Triangle Explanation Examples

A right triangle (literally pronounced "thirty sixty ninety") is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees The triangle is significant because the sides exist in an easytoremember ratio 1 √3 3 2 That is to say, the hypotenuse is twice as long as the shorter leg, and A triangle is a unique right triangle that contains interior angles of 30, 60, and also 90 degrees When we identify a triangular to be a 30 60 90 triangular, the values of all angles and also sides can be swiftly determined Imagine reducing an equilateral triangle vertically, right down the middleThanks to this 30 60 90 triangle calculator you find out that shorter leg is 635 in because a = b√3/3 = 11in * √3/3 ~ 635 in hypotenuse is equal to 127 in because c = 2b√3/3 = 2a ~ 127 in area is 349 in² it's the result of multiplying the legs length and dividing by

Learn About The 30 60 90 Triangle Caddell Prep Online

Red Triangle With Thick White Border Red Triangle Transparent Background Clipart 191 Pikpng

Input one number then click "calculate" button! tan (60) = √3/1 = 173 The right triangle is special because it is the only right triangle whose angles are a progression of integer multiples of a single angle If angle A is 30 degrees, the angle B = 2A (60 degrees) and angle C = 3A (90 degrees)Special Right Triangles in

1

30 60 90 Special Right Triangle Calculator Inch Calculator

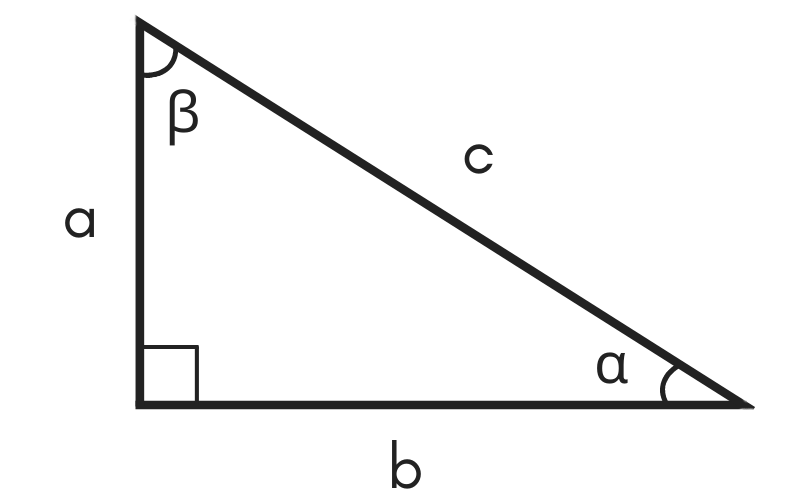
30°60°90° Triangles There is a special relationship among the measures of the sides of a 30 ° − 60 ° − 90 ° triangle A 30 ° − 60 ° − 90 ° triangle is commonly encountered right triangle whose sides are in the proportion 1 3 2 The measures of the sides are x, x 3, and 2 xThis trigonometry video tutorial provides a basic introduction into triangles It explains how to evaluate trigonometric functions such as sine and In a 30°−60°−90° triangle, the length of the hypotenuse is twice the length of the shorter leg, and the length of the longer leg is √3 times the length of the shorter leg To see why this is so, note that by the Converse of the Pythagorean Theorem, these values make the

30 60 90 Right Triangles Free Math Help

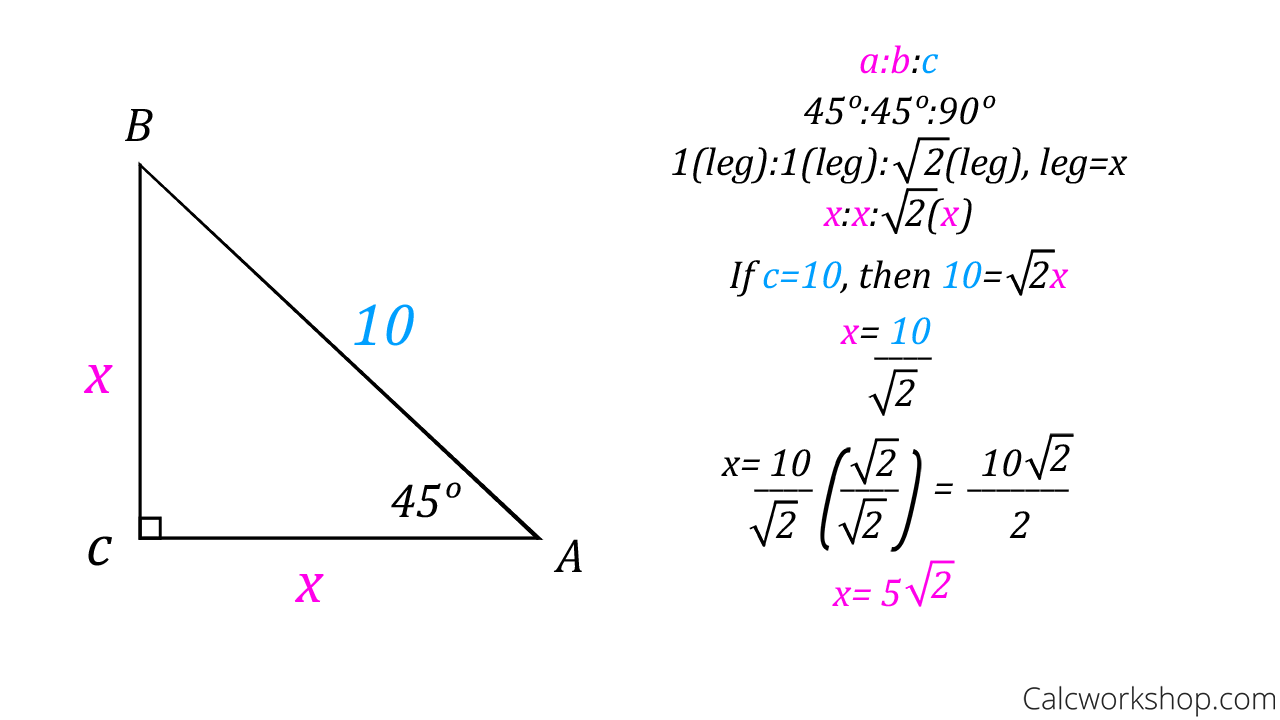
Special Right Triangles Fully Explained W 19 Examples

0 09 what are the ratios of The 30 60 90 refers to the angle measurements in degrees of this type of special right triangle Special right triangles 30 60 90 30 60 90 triangle rules and properties There are two types of special triangles Its properties are so special because it s half of the equilateral triangleSolve the Triangle tri{5}{30}{}{60}{}{90} In any right triangle, Substitute the actual values into the equation Use the power rule to distribute the exponent Tap for more steps Apply the product rule to Apply the product rule to Simplify the numerator Tap for more stepsA 30̊ 60̊ 90̊ right triangle or rightangled triangle is a triangle with angles 30̊ 60̊ 90̊ Formulas of triangle with angle 30̊ 60̊ 90̊ • perimeter = long side short side hypotenuse;

Area Of A Triangle Calculator Calculate Using Sss Sas Asa Ssa Rules

30 60 90 Right Triangle Calculator

$1 per month helps!!For example, a degree triangle could have side lengths of2, 2√3, 47, 7√3, 14√3, 3, 2√3 We can see that this is a right triangle in which the hypotenuse is twice the length of one of the legsMore items•For example, given that the side corresponding to the 60° angle is 5, let a be the length of the side corresponding to the 30° angle, b be the length of the 60° side, and c be the length of the 90° side Angles 30° 60° 90° Ratio of sides 1√ 32 Side lengths a5c Then using the known ratios of the sides of this special type of triangle

30 60 90 Special Right Triangle Calculator Inch Calculator

13 3 2 The 30 60 90 Triangle Graphing Calculator By Mathlab User Manual

 The following diagram shows a triangle and the ratio of the sides 30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another – the ratio is aPack of 2 Large Transparent Metric Triangle Ruler Set Square 30 cm (12 Inch) 30/60 Degree & 22 cm (9 inch) 45/90 Degree Essential for School and Work use (cm Scale) 44 out of 5 stars 73 What is the Triangle rule?

Special Right Triangle 30 60 45 45 37 53 Elearning

30 60 90 And 45 45 90 Triangle Calculator

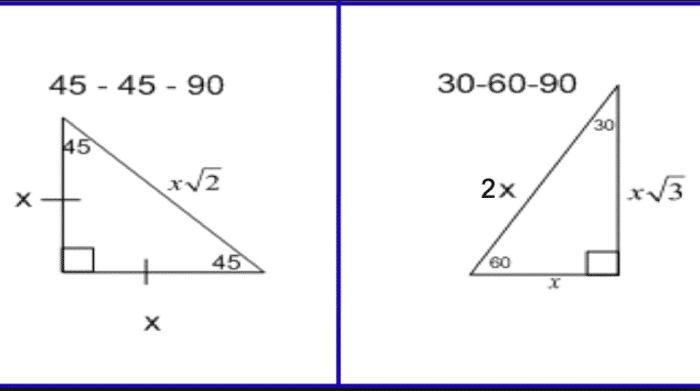
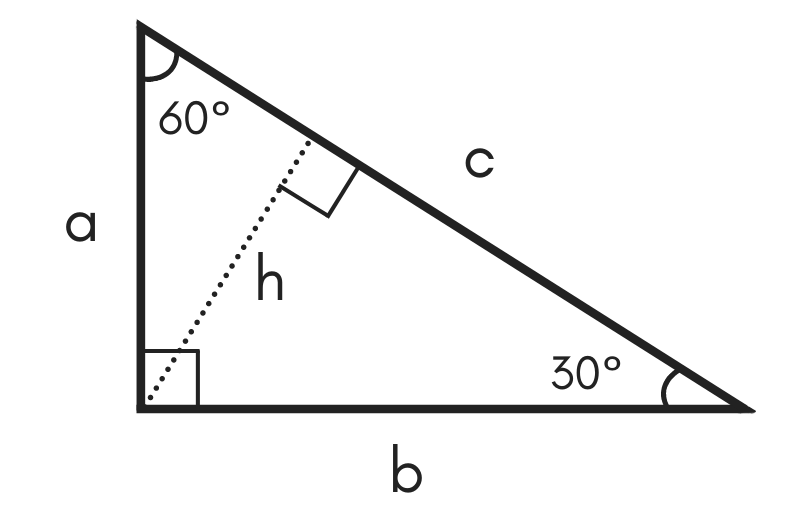
Here is the proof that in a 30°60°90° triangle the sides are in the ratio 1 2 It is based on the fact that a 30°60°90° triangle is half of an equilateral triangle Draw the equilateral triangle ABC Then each of its equal angles is 60° (Theorems 3 and 9) Draw the straight line AD bisecting the angle at A into two 30° angles Since the right angle is always the largest angle, the hypotenuse is always the longest side using property 2 We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a2b2=c2 12(3–√)2=13=4=c2 4–√=2=c 30° 60° 90° x x√3 2x x²√3/2 x(3√3) 30° 60° 45° 45° 90° x x x√2 x²/2 x(2√2) 45° 45° x 2x x 2x x√5 x² x(3√5) ~265° ~635° x 3x x 3x x√10 3x²/2 x(4√10) ~185° ~715° 3x 4x 5x 3x 4x 5x 6x² 12x ~37° ~53°

Special Right Triangles Video Lessons Examples And Solutions

45 45 90 Triangle Calculator Online Discount Shop For Electronics Apparel Toys Books Games Computers Shoes Jewelry Watches Baby Products Sports Outdoors Office Products Bed Bath Furniture Tools Hardware

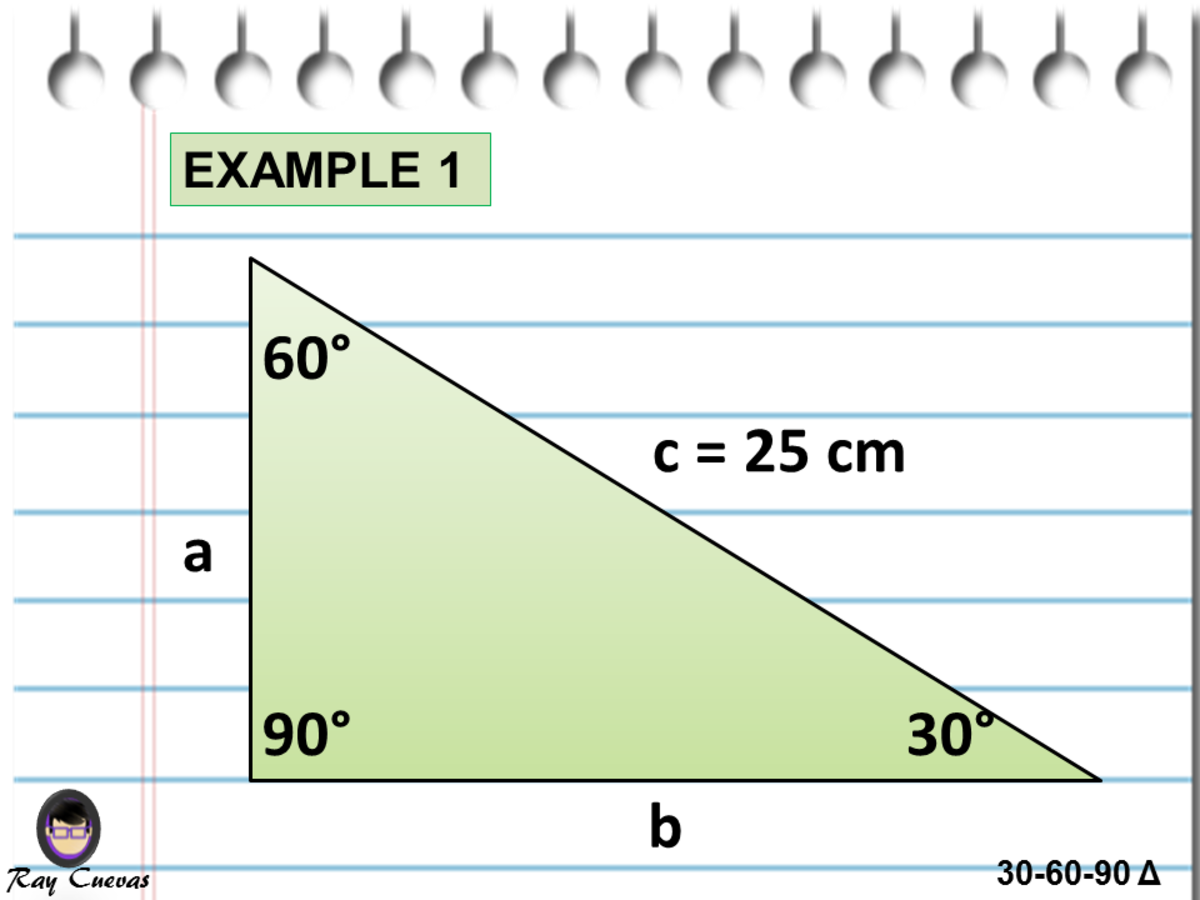
The 30 60 90 right triangle is a special case triangle with angles measuring 30 60 and 90 degrees 30 60 90 triangle in trigonometry And because this is a 30 60 90 triangle and we were told that the shortest side is 8 the hypotenuse must be 16 and the missing side must be 8 3 or 8 3Trigonometry Examples Popular Problems Trigonometry Solve the Triangle tri {} {30} {} {60} {} {90} Side Angle b = c = a = A = 30 B = 60 C = 90 Side Angle b = c = a = A = 30 B = 60 C = 90 There is not enough information to solve for all of the sides and angles of this triangle Unknown triangleThe Triangle Graphing Calculator by MathlabUser Manual 1332 The 30°60°90° Triangle In a 30°60°90° right triangle, the length of the hypotenuse is twice the length of the shorter leg (side opposite the 30° angle) and the length of the longer leg (side opposite the 60° angle) is sqrt (3) times the length of the

Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math

30 60 90 Right Triangle Side Ratios Expii

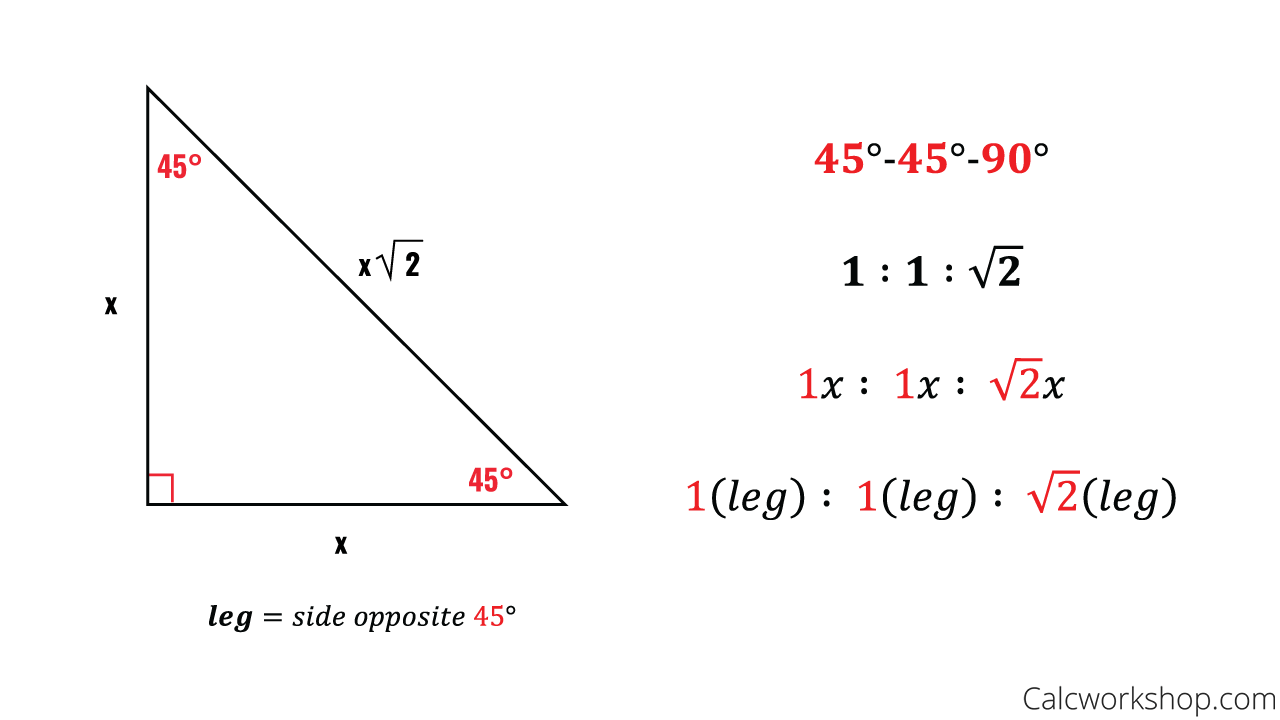
This calculator exists to compute the area of a triangle, where the three angles of the triangle measure 30, 60, and 90 degrees respectively, and only one other measurement is known It works with a measure of any one side, or by inputting the area or perimeterThis may be a 45 45 90 triangle of perhaps a 30 60 90 triangle Recall that with special triangle trigonometry, we do not have to round or use decimals due to the unique ratios between the lengths of the sides However, always remember to simplify your answer by rationalizing the denominator, simplifying the radical or fraction 2The main rule of triangles is that it has one right angle and while the other two angles each measure 45° 45 ° The lengths of the sides adjacent to the right triangle, the shorter sides have an equal length Another rule is that the two sides of the triangle or legs of the triangle that form the right angle are congruent in length

How To Work With 30 60 90 Degree Triangles Education Is Around

What Are The Side Relationships Of A 15 75 90 Triangle Quora

Right Triangle Calculator Although all right triangles have special features – trigonometric functions and the Pythagorean theorem The most frequently studied right triangles , the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 trianglesThanks to all of you who support me on Patreon You da real mvps!30 60 90 Triangle Rules To fully solve our right triangle as a 30 60 90, we have to first determine that the 3 angles of the triangle are 30, 60, and 90 To solve for the side lengths, a minimum of 1 side length must already be known

Special Right Triangles Complete Reference Guide The Education

The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet

 About Triangle A triangle is a unique right triangle whose angles are 30º, 60º, and 90º The triangle is unique because its side sizes are always in the proportion of 1 √ 32 Any triangle of the kind can be fixed without applying longstep approaches such as the Pythagorean Theorem and trigonometric featuresExample of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units in30 60 90 triangle rules and properties The most important rule to remember is that this special right triangle has one right angle and its sides are in an easytoremember consistent relationship with one another the ratio is a a√3 2a

30 60 90 Special Right Triangle Calculator Inch Calculator

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

• area = 05 * long side *Special Right Triangles 30°60°90° triangle The 30°60°90° refers to the angle measurements in degrees of this type of special right triangle In this type of right triangle, the sides corresponding to the angles 30°60°90° follow a ratio of 1√ 32 Thus, in this type of triangle, if the length of one side and the side's

30 60 90 Triangle Explanation Examples

Right Angled Triangle Calculator

30 60 90 Triangle Theorem Ratio Formula Video

Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems

Special Right Triangles Fully Explained W 19 Examples

30 60 90 Triangle Theorem Ratio Formula Video

A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

Special Right Triangles 30 60 90 And 45 45 90 Triangles Youtube

Right Triangles Gmat Free

The Easy Guide To The 30 60 90 Triangle

Triangle Calculator

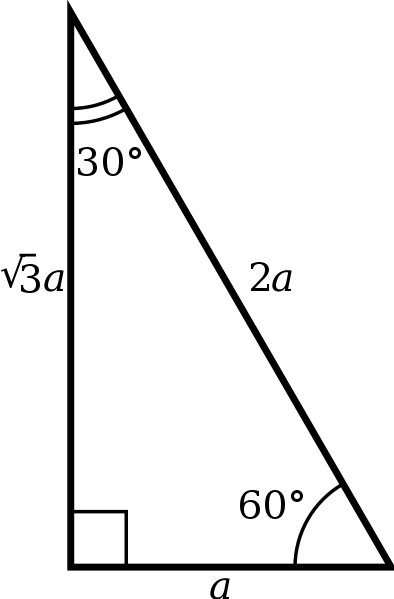
30 60 90 Triangle Formulas Rules And Sides Science Trends

Triangle Calculator

30 60 90 And 45 45 90 Triangle Calculator

1

3

30 60 90 Triangle Rules Calculator Formula The Free Calculator

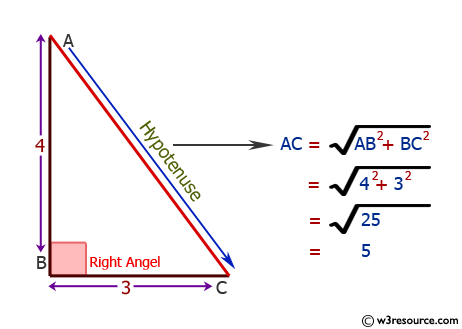
Python Calculate The Hypotenuse Of A Right Angled Triangle W3resource

30 60 90 And 45 45 90 Triangle Calculator

How To Work With 30 60 90 Degree Triangles Education Is Around

30 60 90 Special Right Triangle Calculator General Knowledge Book Right Triangle Electrical Engineering Books

Special Right Triangles Review Article Khan Academy

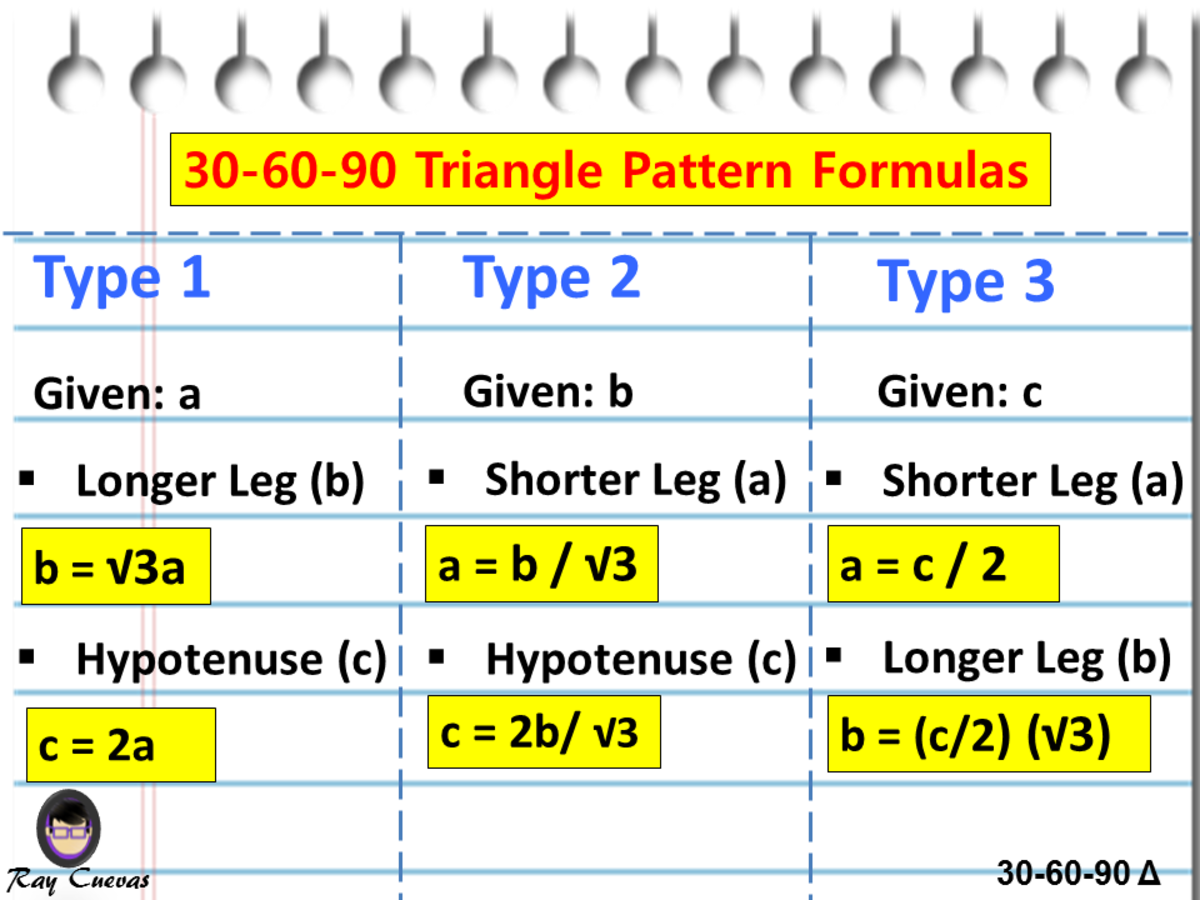
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

30 60 90 Triangle Definition Theorem Formula Examples

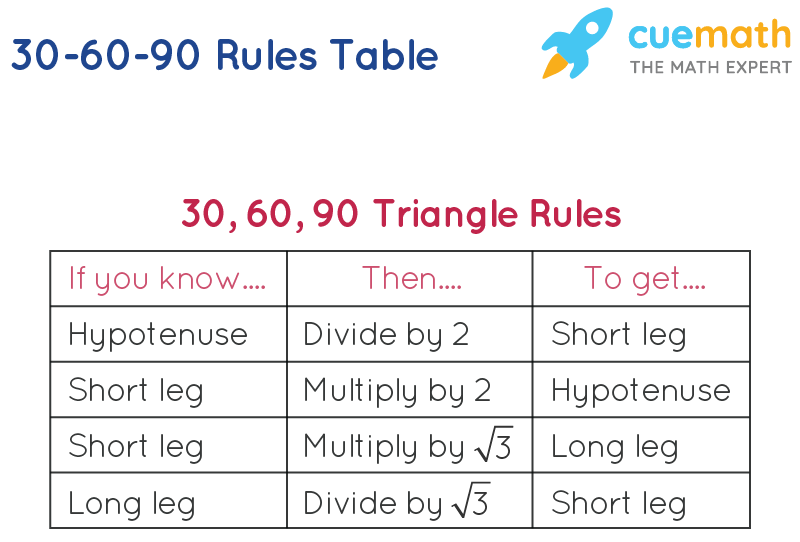
30 60 90 Formula Learn Formula For Calculating The 30 60 90 Measures

30 60 90 Triangle Calculator Formula Rules

A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

30 60 90 Triangle Calculator Purecalculators

30 60 90 Triangle Theorem Ratio Formula Video

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

The Easy Guide To The 30 60 90 Triangle

Triangle Calculator

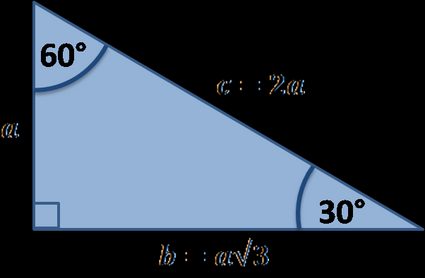
30 60 90 Triangle Calculator Formula Rules

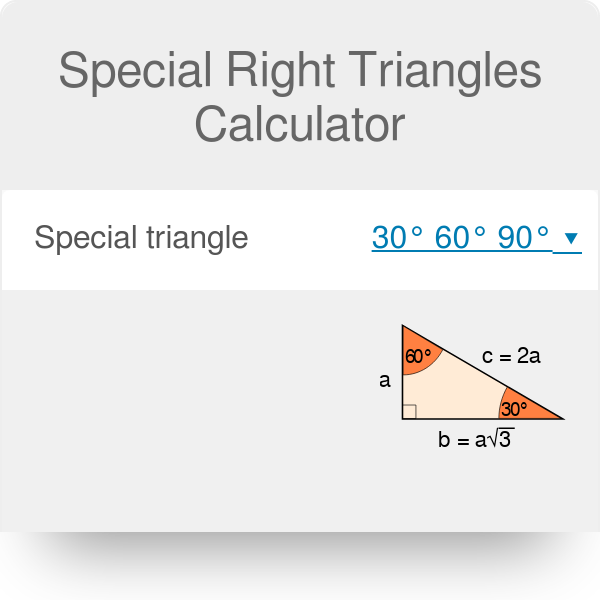
Special Right Triangles Calculator Formula Rules

Triangle 30 60 Calculator Endmemo

A Quick Guide To The 30 60 90 Degree Triangle Dummies

45 45 90 Triangle Theorem Rules Formula Video Lesson Transcript Study Com

30 60 90 Triangle Calculator Formula Rules

30 60 90 Triangle Calculator Formula Rules

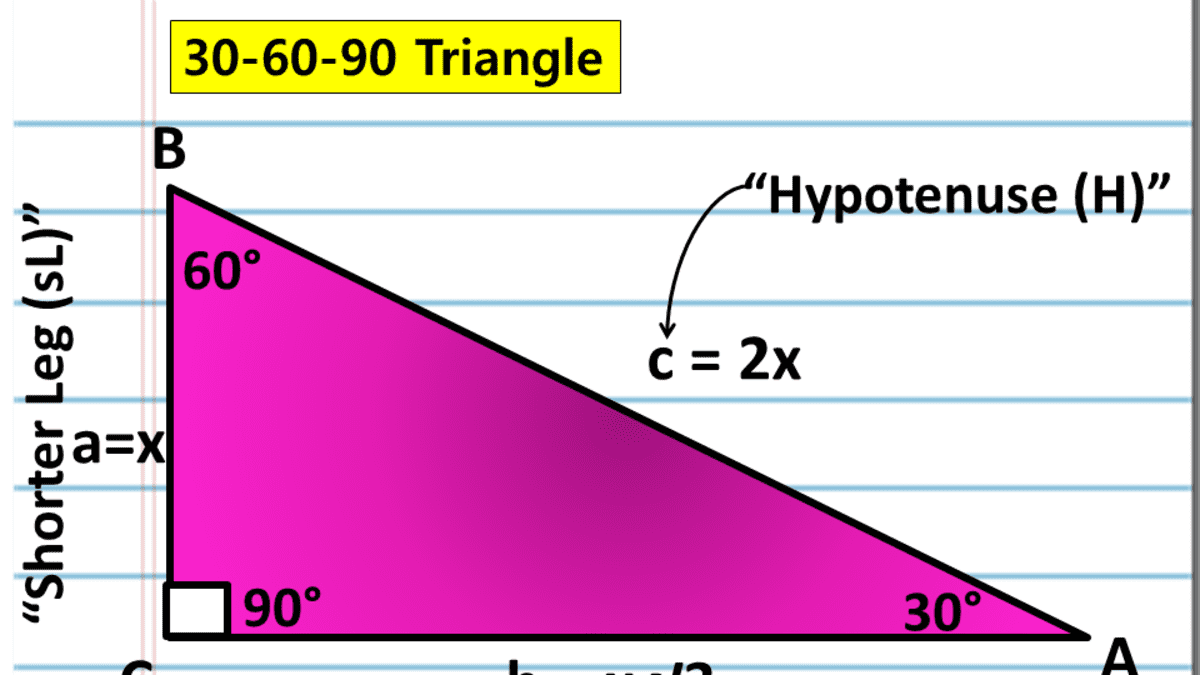
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

Special Right Triangles

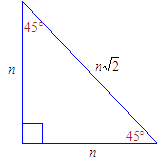
Special Triangles Isosceles And 30 60 90 Calculator

30 60 90 Triangle Example Problem Video Khan Academy

Special Right Triangles Part 1 45 45 90 And 30 60 90 Youtube

30 60 90 Triangle Theorem Proof Don T Memorise Youtube

30 60 90 Triangle Rules Calculator Formula The Free Calculator

30 60 90 Triangle Calculator Formula Rules

30 60 90 Triangle Definition Theorem Formula Examples

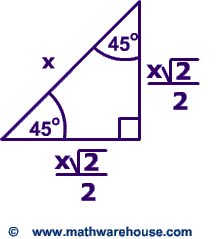
Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems

30 60 90 Triangle Calculator Formula Rules

The Complete Guide To The 30 60 90 Triangle

30 60 90 Triangles Special Right Triangle Trigonometry Youtube

30 60 90 Triangle Theorem Ratio Formula Video

The Complete Guide To The 30 60 90 Triangle

30 60 90 Special Right Triangle Calculator Inch Calculator

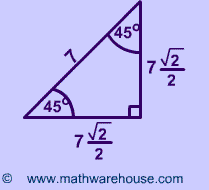
Special Right Triangles Formulas 30 60 90 And 45 45 90 Special Right Triangles Examples Pictures And Practice Problems

The Easy Guide To The 30 60 90 Triangle

A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

1

45 45 90 Triangle Calculator Formula Rules

30 60 90 Right Triangles Solutions Examples Videos

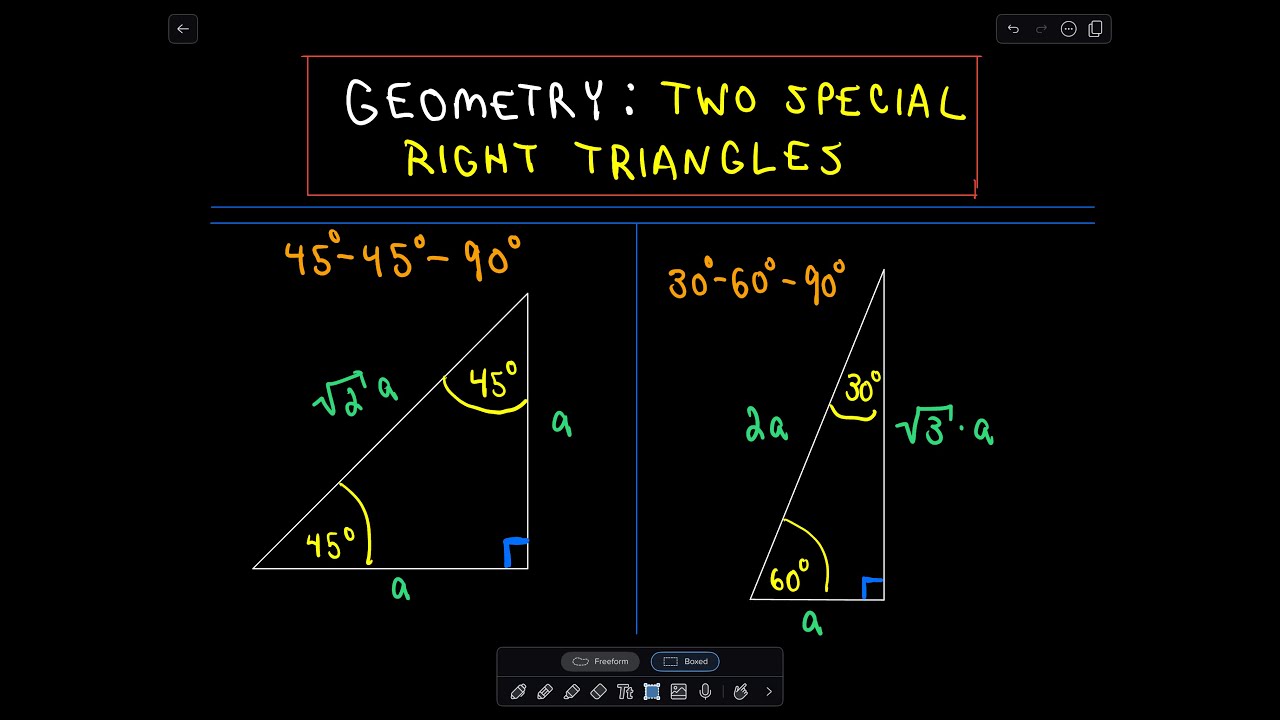
Special Right Triangles In Geometry 45 45 90 And 30 60 90 Youtube

Triangle Calculator

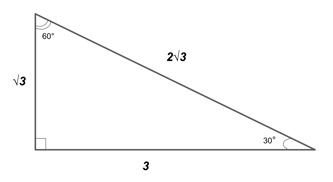
The Easy Guide To The 30 60 90 Triangle

How To Work With 30 60 90 Degree Triangles Education Is Around

30 60 90 Triangle Rules Calculator Formula The Free Calculator

Triangle Calculator

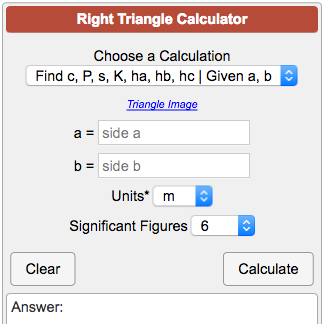
Right Triangles Calculator

30 60 90 And 45 45 90 Triangle Calculator

Right Triangles Gmat Free

30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com

30 60 90 Triangle Formulas Rules And Sides Science Trends

How To Work With 30 60 90 And 45 45 90 Degree Triangles Dummies

A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

30 60 90 Triangle Theorem Ratio Formula Video

30 60 90 Triangle Theorem Ratio Formula Video

13 3 2 The 30 60 90 Triangle Graphing Calculator By Mathlab User Manual

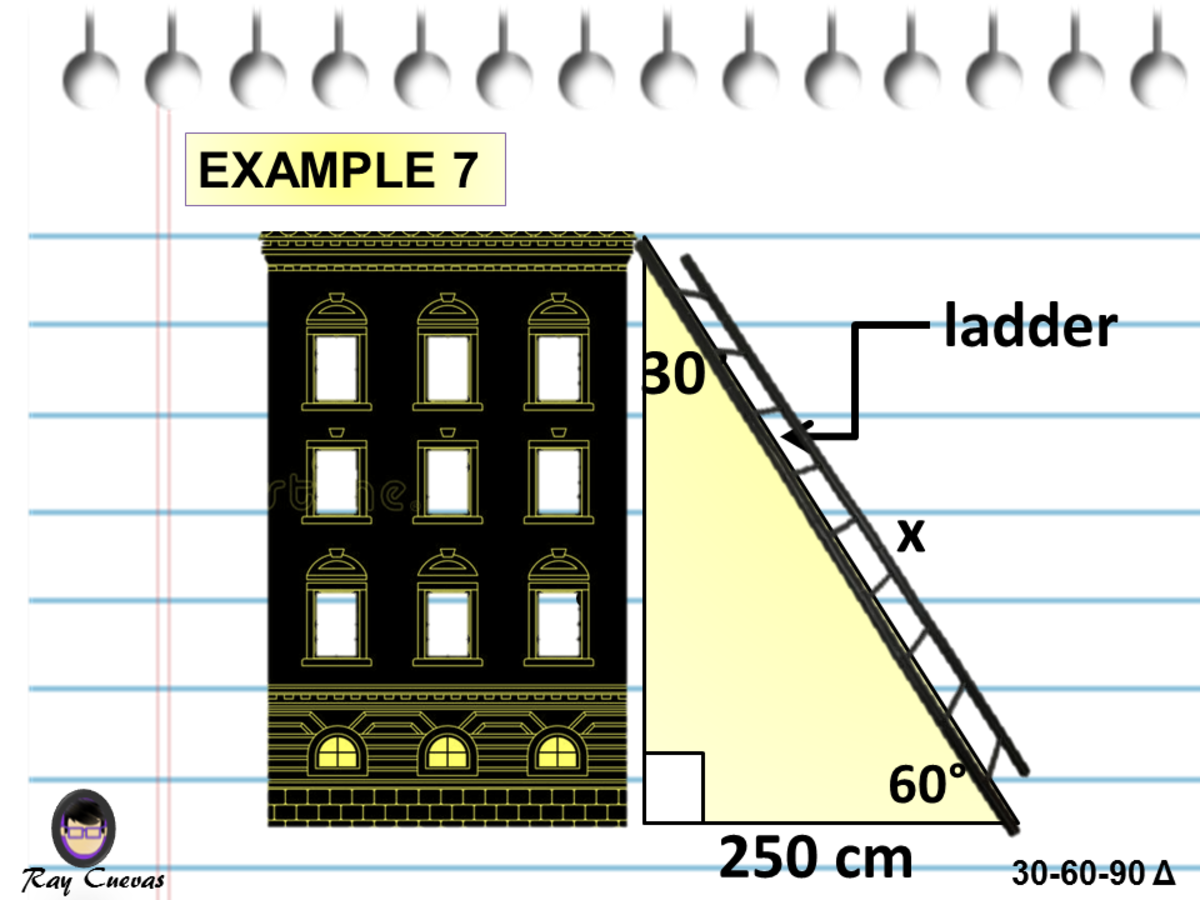
A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation

30 60 90 Triangle Theorem Ratio Formula Video

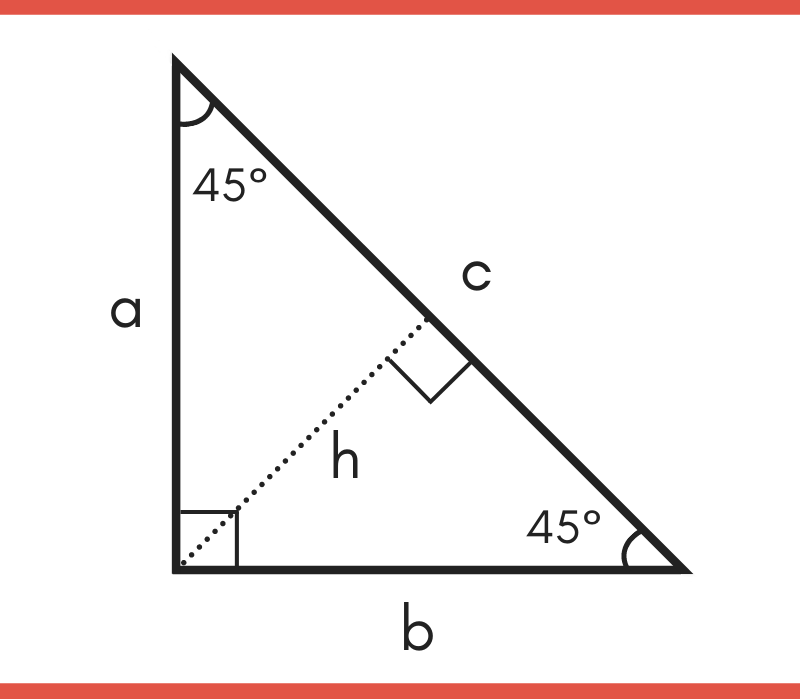
45 45 90 Special Right Triangle Calculator Inch Calculator